The Four Color Map Theorem: A Journey Through Color And Topology

The Four Color Map Theorem: A Journey Through Color and Topology

Related Articles: The Four Color Map Theorem: A Journey Through Color and Topology

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to The Four Color Map Theorem: A Journey Through Color and Topology. Let’s weave interesting information and offer fresh perspectives to the readers.

The Four Color Map Theorem: A Journey Through Color and Topology

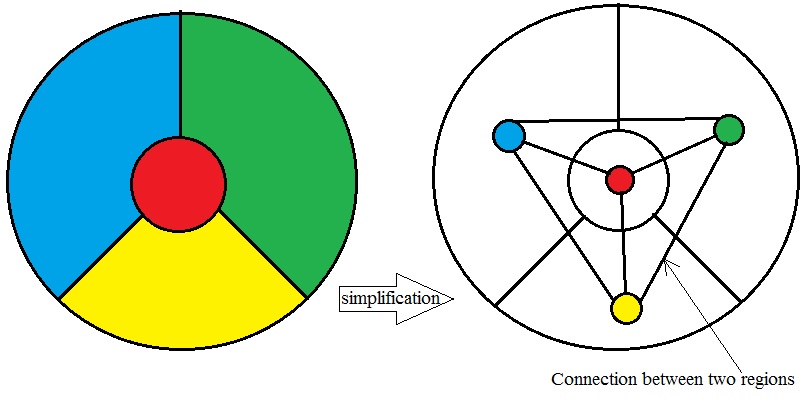
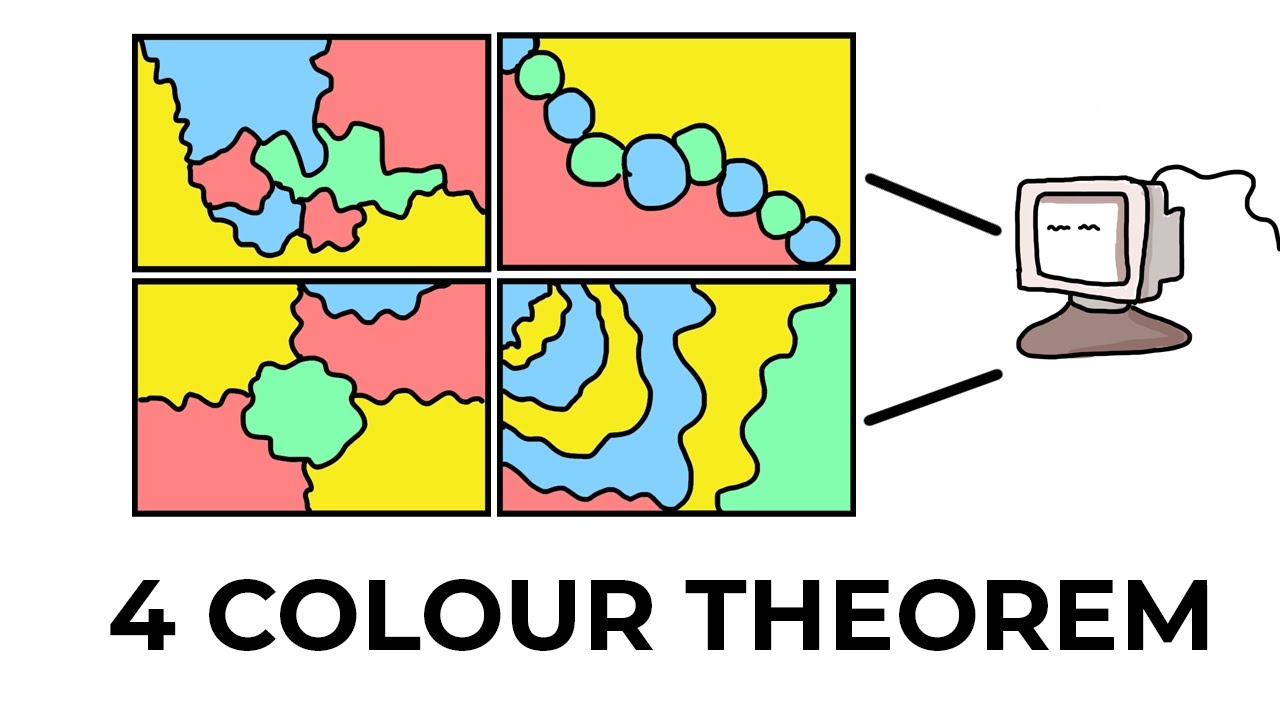
The world is a tapestry of colors, and maps, as representations of that world, are often adorned with vibrant hues. Yet, beneath the aesthetic appeal, lies a fascinating mathematical theorem that governs the very essence of color allocation on maps: the Four Color Map Theorem.

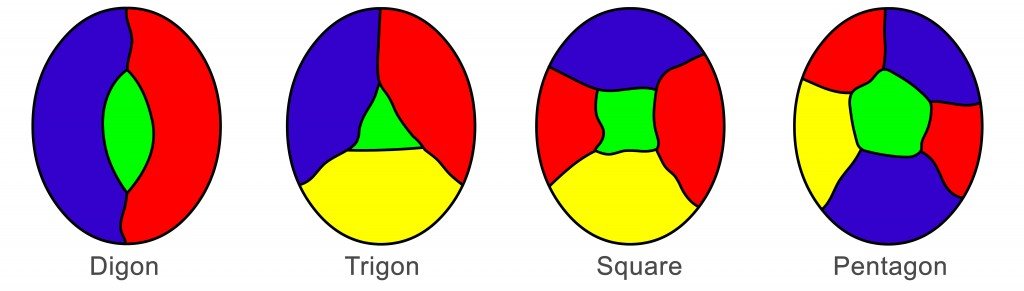
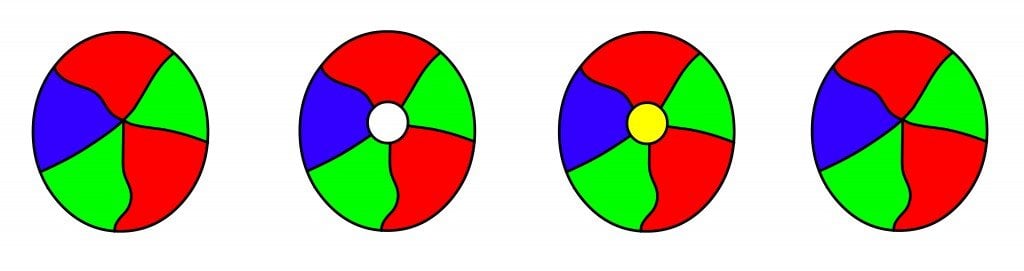
This theorem, a cornerstone of graph theory and topology, states that any map drawn on a plane, or a sphere, can be colored using only four colors in such a way that no two adjacent regions share the same color. While seemingly simple, this theorem has captivated mathematicians for over a century, its proof a testament to the power of abstract reasoning and the intricate relationship between color and geometry.

Unveiling the Roots: A Historical Perspective

The origins of this theorem can be traced back to 1852, when Francis Guthrie, a young English mathematician, noticed that he could color the counties of England using only four colors without any two adjacent counties sharing the same color. This observation, initially dismissed as a curious quirk, sparked a question that would ignite a mathematical firestorm: could this principle be generalized to any map, regardless of its complexity?

The question, though deceptively simple, proved to be remarkably difficult to answer. Mathematicians across the globe engaged in a century-long quest to prove or disprove the four color conjecture, as it was then known. The problem, seemingly trivial, was a formidable foe, resisting numerous attempts at a solution.

The Triumph of Proof: A Collaborative Effort

The path to proving the four color conjecture was paved with numerous false starts and dead ends. The challenge lay not only in the complexity of the problem itself but also in the lack of suitable mathematical tools to tackle it.

Finally, in 1976, Kenneth Appel and Wolfgang Haken, using a revolutionary approach involving computer algorithms, were able to prove the conjecture, thereby elevating it to the status of a theorem. Their proof, however, was met with skepticism and controversy. Critics argued that relying on computer assistance to verify a mathematical theorem was not a rigorous method.

The debate surrounding the computer-assisted proof highlighted the evolving nature of mathematics. The increasing reliance on computational methods in proving complex theorems was a paradigm shift, challenging traditional notions of mathematical rigor. Despite the initial controversy, the proof, after rigorous scrutiny, was eventually accepted by the mathematical community.

Beyond Maps: Applications in Diverse Fields

The Four Color Map Theorem, while rooted in the seemingly mundane realm of map coloring, has far-reaching implications in diverse fields, demonstrating its profound impact beyond its initial context.

• Graph Theory: The theorem finds its most direct application in graph theory, a branch of mathematics that studies relationships between objects represented as points (vertices) connected by lines (edges). Maps can be represented as graphs, with regions corresponding to vertices and shared boundaries to edges. The theorem’s principle of coloring adjacent regions differently translates to coloring adjacent vertices in a graph, ensuring that no two connected vertices share the same color. This principle has applications in scheduling, network design, and resource allocation.

• Computer Science: The theorem’s proof, relying heavily on computer algorithms, has spurred advancements in computer science. The development of algorithms to check for valid colorings of maps has contributed to the development of efficient algorithms for solving similar problems in various fields.

• Computer Graphics: The theorem’s principles have been applied in computer graphics to color objects in three-dimensional space, ensuring that adjacent objects do not have the same color. This has applications in creating realistic visuals for games, movies, and scientific simulations.

• Data Visualization: The theorem’s principles can be used to create visually appealing and informative data visualizations. By assigning different colors to different categories of data, it ensures that data is presented clearly and effectively.

FAQs about the Four Color Map Theorem

1. Can the theorem be applied to maps with more than four colors?

While the theorem states that four colors are sufficient to color any map, it does not preclude the use of more than four colors. In practice, maps often use more than four colors for aesthetic purposes or to distinguish specific regions. However, the theorem guarantees that four colors are always enough to avoid conflicts between adjacent regions.

2. Does the theorem apply to maps drawn on surfaces other than a plane or a sphere?

The theorem is specifically applicable to maps drawn on a plane or a sphere. For maps drawn on other surfaces, such as a torus (donut shape), the theorem does not hold. For instance, a map drawn on a torus can require up to seven colors to avoid conflicts between adjacent regions.

3. What is the significance of the computer-assisted proof?

The computer-assisted proof of the Four Color Map Theorem was a significant event in the history of mathematics. It demonstrated the increasing role of computers in proving complex theorems, challenging traditional notions of mathematical rigor. It also highlighted the importance of collaboration between mathematicians and computer scientists in tackling complex problems.

4. Are there any practical applications of the theorem in everyday life?

While the theorem itself may not have direct practical applications in everyday life, the principles underlying it have applications in various fields. For example, the concept of coloring adjacent regions differently is applied in scheduling, network design, and resource allocation.

Tips for Understanding the Four Color Map Theorem

• Visualize the concept: Start by drawing a simple map and try coloring it using only four colors. This will help you grasp the theorem’s basic principle.

• Explore different types of maps: Examine maps with varying complexities and try to color them using only four colors. This will help you understand the theorem’s universality.

• Learn about graph theory: Understanding the relationship between maps and graphs will enhance your comprehension of the theorem’s applications beyond map coloring.

• Read about the history of the theorem: Understanding the journey to proving the theorem will provide a deeper appreciation for its significance.

Conclusion

The Four Color Map Theorem, a seemingly simple mathematical statement, has captivated mathematicians for over a century, its proof a testament to the power of human ingenuity and the intricate relationship between color and geometry. The theorem’s impact extends far beyond the realm of map coloring, finding applications in diverse fields, from computer science and data visualization to network design and scheduling. Its legacy serves as a reminder of the enduring power of mathematics to illuminate the hidden structures and patterns that govern our world.

Closure

Thus, we hope this article has provided valuable insights into The Four Color Map Theorem: A Journey Through Color and Topology. We thank you for taking the time to read this article. See you in our next article!