Unveiling the Power of Three-Variable Karnaugh Maps: A Comprehensive Guide
Related Articles: Unveiling the Power of Three-Variable Karnaugh Maps: A Comprehensive Guide
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Power of Three-Variable Karnaugh Maps: A Comprehensive Guide. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unveiling the Power of Three-Variable Karnaugh Maps: A Comprehensive Guide
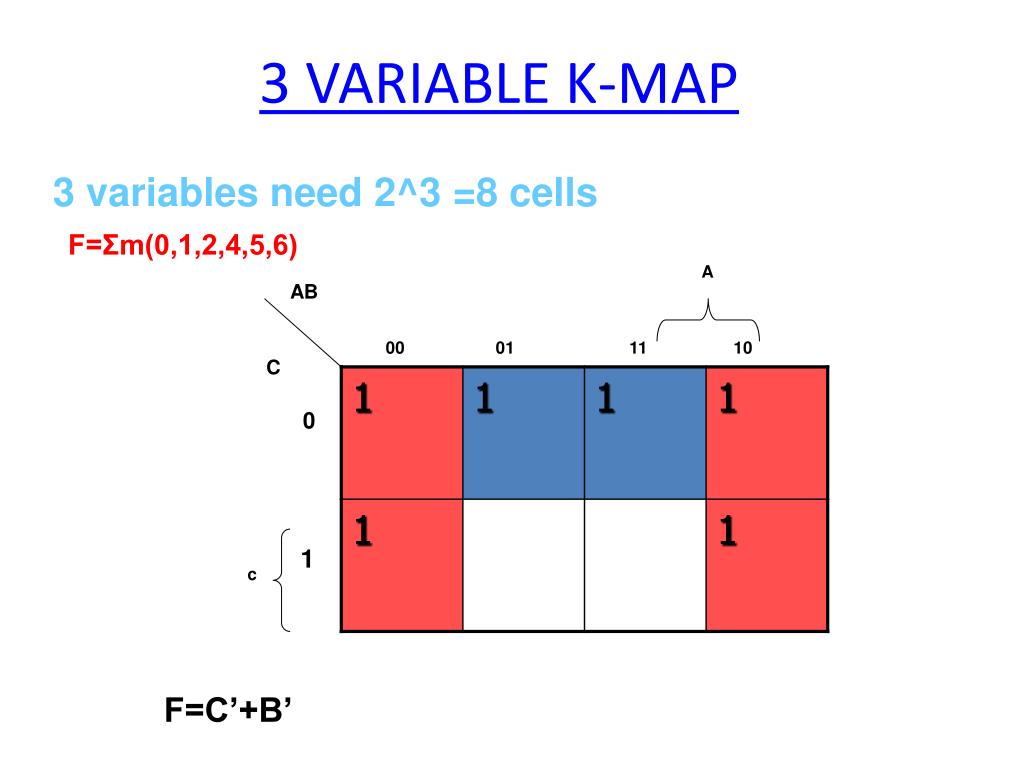
The realm of digital logic design thrives on efficient methods for simplifying complex Boolean expressions. Among the powerful tools employed, the Karnaugh map, named after its inventor Maurice Karnaugh, stands out as a visual and intuitive approach. This article delves into the intricacies of three-variable Karnaugh maps, exploring their construction, utilization, and profound impact on logic circuit optimization.
Understanding the Fundamentals
A Karnaugh map, in essence, is a graphical representation of a truth table. It provides a structured framework for visually identifying and grouping adjacent minterms, ultimately leading to a simplified Boolean expression. Each cell within the map represents a unique combination of input variables, while the value within the cell indicates the corresponding output value.
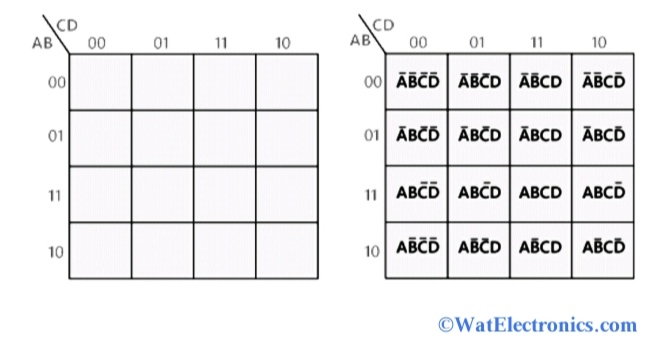
The Three-Variable Karnaugh Map: A Visual Journey
A three-variable Karnaugh map is a two-dimensional grid consisting of four rows and four columns, as shown below:
| 00 | 01 | 11 | 10 | |
|---|---|---|---|---|
| 0 | ||||
| 1 | ||||
| 3 | ||||
| 2 |
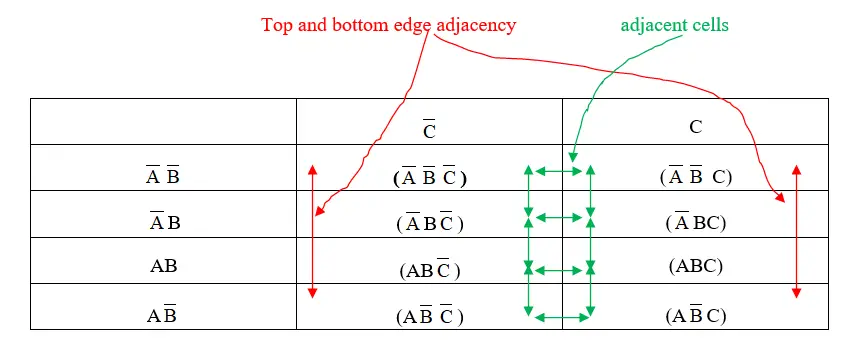
Each row represents a specific value for the third variable, typically denoted as C, while the columns represent the combinations of the first two variables, A and B. The binary values assigned to each row and column are arranged in a Gray code sequence, ensuring that only one variable changes between adjacent cells. This arrangement facilitates the identification of adjacent minterms, a crucial step in simplification.
Populating the Map: A Step-by-Step Approach
- Truth Table Conversion: Begin by constructing the truth table for the Boolean function you intend to simplify. The truth table lists all possible input combinations and their corresponding output values.
- Mapping the Outputs: For each input combination in the truth table, locate the corresponding cell in the Karnaugh map and enter the output value (0 or 1) within that cell.
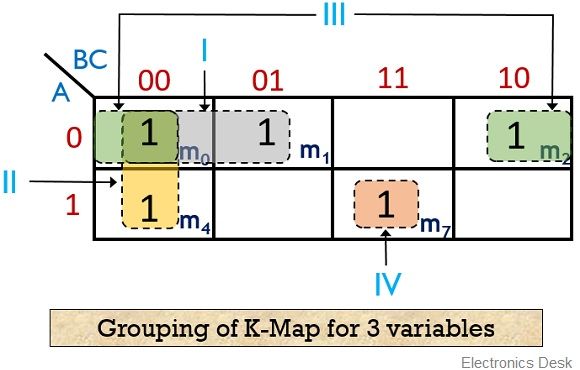
- Visualizing the Adjacency: Once the map is populated, carefully observe the arrangement of 1’s within the map. Adjacent cells, either horizontally or vertically, represent minterms that differ by only one variable. These adjacent 1’s can be grouped together.
The Art of Simplification: Looping for Efficiency
The true power of Karnaugh maps lies in their ability to simplify Boolean expressions by grouping adjacent 1’s. This grouping, known as looping, is guided by the following principles:
- Loop Size: The larger the loop, the more variables are eliminated from the simplified expression.
- Power of Two: Loops must contain a number of 1’s that is a power of two (1, 2, 4, 8, etc.).
- Overlapping Loops: Loops can overlap, allowing for the inclusion of 1’s in multiple groups.
- Corner Adjacency: Cells in the corners of the map are considered adjacent.
Deriving the Simplified Expression:
Once the loops are identified, each loop corresponds to a product term (AND gate) in the simplified expression. The variables within each loop are determined by noting the common variables across all cells within the loop. If a variable appears in both its complemented and uncomplemented form within a loop, it is excluded from the product term.
Illustrative Example:
Let’s consider the Boolean function F(A, B, C) = Σm(0, 2, 4, 5, 6). This function is represented by the following truth table:
| A | B | C | F |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Mapping the Function:
The Karnaugh map for this function is:
| 00 | 01 | 11 | 10 | |
|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 3 | 0 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 |
Identifying the Loops:
We can identify two loops in this map:
- Loop 1: Encompassing cells (0, 2, 4, 6) with a value of 1, representing the product term A’C’.
- Loop 2: Encompassing cells (4, 5, 6) with a value of 1, representing the product term BC’.
The Simplified Expression:
The simplified expression for the function F(A, B, C) is obtained by combining the product terms from each loop:
F(A, B, C) = A’C’ + BC’
Benefits of Using Karnaugh Maps:
- Simplified Boolean Expressions: Karnaugh maps effectively eliminate redundant terms, leading to concise and optimized Boolean expressions.
- Visual Intuition: The visual nature of Karnaugh maps provides an intuitive understanding of the relationships between variables and their impact on the output.
- Reduced Logic Complexity: Simplified expressions translate to simpler logic circuits, reducing the number of gates required and improving circuit performance.
- Error Detection: Karnaugh maps facilitate the identification of potential errors in the Boolean expression, ensuring accuracy in logic design.
FAQs: Addressing Common Queries
Q: What is the purpose of the Gray code arrangement in Karnaugh maps?
A: The Gray code arrangement ensures that only one variable changes between adjacent cells. This property simplifies the identification of adjacent minterms, facilitating the grouping process.
Q: Can I use Karnaugh maps for more than three variables?
A: While Karnaugh maps are commonly used for three variables, their visual representation becomes complex for higher numbers of variables. For four variables, a two-dimensional map can be used, but for five or more variables, other methods like the Quine-McCluskey algorithm become more practical.
Q: How do I handle "don’t care" conditions in Karnaugh maps?
A: "Don’t care" conditions, denoted by "X" in the map, represent input combinations that are not relevant to the function. They can be used to enhance simplification by incorporating them into loops, effectively expanding their size and further reducing the expression.
Tips for Successful Karnaugh Mapping:
- Start with a Clear Truth Table: Ensure the truth table accurately reflects the desired function.
- Practice Gray Code: Familiarize yourself with the Gray code sequence to navigate the map efficiently.
- Identify All Loops: Don’t miss any potential loops, as they can contribute to further simplification.
- Prioritize Larger Loops: Focus on grouping 1’s into the largest possible loops to maximize simplification.
- Validate the Result: After deriving the simplified expression, verify its correctness by comparing it to the original truth table or Boolean expression.
Conclusion: A Powerful Tool in Logic Design
Three-variable Karnaugh maps offer a powerful and intuitive approach to simplifying Boolean expressions. Their visual nature and systematic grouping process make them invaluable for logic circuit optimization, leading to reduced complexity, improved performance, and enhanced circuit efficiency. By mastering the techniques of Karnaugh mapping, designers can effectively translate complex Boolean functions into concise and practical logic circuits. This visual tool serves as a testament to the elegance and power of graphical methods in the field of digital logic design.





Closure
Thus, we hope this article has provided valuable insights into Unveiling the Power of Three-Variable Karnaugh Maps: A Comprehensive Guide. We thank you for taking the time to read this article. See you in our next article!
